Fonctionnement d'un réseau de neurone artificiel

Une explication simple sur le principe de fonctionement d’un réseau de neurone, outil de machine learning qui permet d’approximer des fonctions.

Le réseau de neurone est une méthode utilisée en machine learning, pour la regression ou la classification de données. La régression est l’approximation d’une fonction réelle (par exemple les prix d’un logement, que l’on veut approximer en fonction de sa localisation géographique). La classification consiste à attribuer des labels à des données : par exemple, en fonction de la couleur et de la forme d’un champignon, déterminer s’il est toxique ou pas (2 labels ici : Toxique, non toxique).

Le neurone.

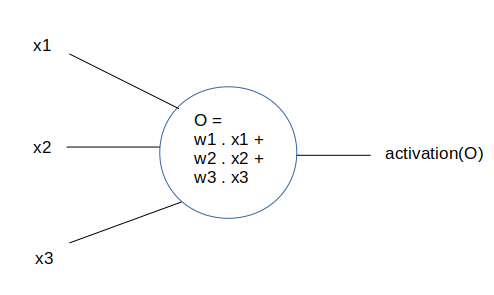
Un neurone est tout simplement une fonction, dotée de paramètres.

Cette fonction est \(output = activation(w_1 x1 + w_2 x2 + ... + w_n x_n)\).

L’entrée (input) est fournies par les données, ou bien par les sorties des neurones précédents. C’est le vecteur \((x_1, x_2, .. x_n)\)

Les poids du neurone sont les valeurs \((w_1, w_2, .. w_n)\). Ce sont les seuls valeurs qui sont propres au réseau de neurone. Lorsque l’on sauvegardera sur le disque notre réseau entrainé, ce seront ces poids qui seront enregistrés. Les poids d’un réseau de neurone, avec son architecture (nombre de couches, nombre de neurones sur chaque couche), le définissent entièrement.

La sortie (output), est un nombre réel, donné par la fonction ci-dessus.

Et la fonction d’activation est une fonction non linéaire. Nous verrons plus bas les différentes fonctions d’activation habituellement utilisées.

Le réseau

Un réseau est constitué habituellement de couches successives de neurones placés en parallèle.

Chaque neurone prend son entrée depuis la sortie des neurones de la couche suivante. On appelle “fully connected layer” lorsque pour chaque neurone, sa sortie est reliée à tous les neurones de la couche suivante.

Il existe d’autres types de couche, ou les neurones ne sont pas nécessairement connectés à tous les neurones de la couche précédentes. Un exemple est le réseau de neurone convolutif (convolutional neural network), qui est particulièrement adapté pour le traitement d’images en raison de son architecture.

Les fonctions d’activation

Si on utilise la fonction identité (\(f(x) = x\)), alors le neurone représentera une simple combinaison linéaire des input, et des poids.

En général, on utilise des fonctions non linéaires. Deux fonctions parmi les plus courantes sont la sigmoide, et reLu :

La sigmoïde

La fonction ReLU a pour équation

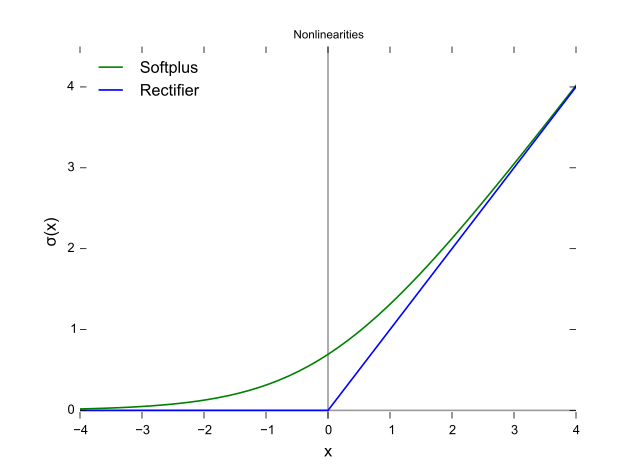
Elle est représentée en bleu sur l’image ci-dessus. Ces différentes fonctions peuvent avoir une influence sur la performance du réseau de neurone à généraliser à partir des données qui lui sont fournies.

Pourquoi des fonctions d’activations non linéaires ?

On peut se demander pourquoi un réseau de neurone a-t-il besoin de ces fonctions d’activations non linéaires. C’est précisément cette non linéarité qui donne toute sa puissance au réseau de neurone, et le rend capable d’approximer n’importe quelle fonction continue.

En fait, un réseau de neurone sans ces non linéarités, avec uniquement des combinaisons linéaires, n’a aucune utilité, car il peut être simplifié lui même en une combinaison linéaire. Ajouter des couches n’a aucune influence sur la puissance de représentation du réseau.

Vous pouvez lire ici une preuve (en anglais) visuelle du fait que les réseaux de neurones sont des approximateurs universels (ils peuvent s’approcher de toute fonction continue).

FeedForward

Un réseau de neurone est utilisé en regression ou classification. Pour l’utiliser, on utilise l’opération de “forward” : il s’agit de calculer la sortie du réseau de neurone en fonction de l’entrée, en appliquant couche par couche les fonctions des neurones.

Pour obtenir une bonne valeur de sortie, il est donc nécessaire de configurer les paramtres des neurones (appelés “poids”) pour qu’à chaque sample (une instance de nos données), une valeur convenable lui soit associée.

Backpropagation

L’entrainement d’un réseau de neurone est effectué habituellement par l’algorithme de backpropagation, basé sur la descente du gradient.

Pour chaque sample (input, value), on calcule le loss \(L\) (par exemple le carré de la différence entre la sortie du réseau de neurone, et la valeur voulue) : \(L = \lVert value - output \rVert^2\).

Pour chaque poids \(w\), on calcule le gradient de cette fonction \(L\) en fonction des poids du neurone. On commence par la dernière couche, puis les couches précedentes grâce à la relation de chaine. On obtient ainsi pour chaque poids \(w\) la valeur du gradient au point donnée par le sample.

Puis on applique l’algorithme de la descente du gradient pour modifier légerement les poids du réseau de neurone

\(\lambda\) est appelé facteur d’apprentissage ou learning rate. Plus le learning rate est faible, plus le réseau apprendra lentement. Mais un learning rate trop grand peut empêcher la convergence des poids. En général, on choisit une valeur \(\lambda \leq 0.1\)

Pour avoir un détail des calculs, vous pouvez consulter le site suivant : http://neuralnetworksanddeeplearning.com/chap2.html