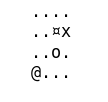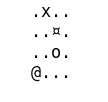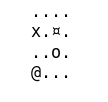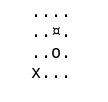
Cet article est la suite de /2017/08/18/reinforcement-learning-part1/.

Dans cette deuxième partie, nous allons travailler encore sur le même jeu, mais en utilisant un réseau de neurone au lieu d’un tableau de valeurs.

Plan

• Partie 1 : jeu statique, le terrain ne change pas, utilisation d’un tableau de valeurs (sans réseau de neurones).
• Partie 2 : Jeu statique, le terrain ne change pas, utilisation d’un réseau de neurone pour approximer la fonction de valeurs Q.
• Partie 3 : Jeu dynamique, le terrain change à chaque partie : utilisation d’un réseau de neurones.

Ici, nous allons modéliser la fonction de valeurs Q grâce à un réseau de neurones. Cela nous permet de ne pas maintenir un tableau qui contient les valeurs de Q pour chaque état et chaque action, ce qui va s’avérer très utile lorsque nous aurons un grand nombre d’états (comme pour la partie 3, ou le terrain sera modifié à chaque partie).

Vous pouvez retrouver tout le code décrit dans cet article sur github.

Le jeu

Identique, voir Partie 1 : Un terrain est fixé, avec la position des éléments. Puis l’agent doit apprendre comment gagner le maximum de points en se déplaçant sur ce terrain.

Le réseau de neurone

Pour implémenter le réseau de neurone, nous utiliserons la librairie open source Keras, qui est une interface haut niveau à des librairies comme TensorFlow. Elle nous permet de créer des réseaux de neurone très simplement.

Nous allons définir une classe “trainer”, qui sera l’interface avec le réseau de neurone.

Les paramètres de cette classe seront :

• les dimensions du réseau
• le facteur d’actualisation \(\gamma\). Il apparait dans la formule d’actualisation du Q learning : \(Q(s, a) = r(s, a) + \gamma * max(Q(s', a'))\)
• Le learning rate \(\alpha\). Ce sera le learning rate de l’algorithme d’apprentissage du réseau de neurone.
• Le facteur d’exploration \(\epsilon\), et son coefficient multiplicateur (entre 0 et 1). A chaque étape, \(\epsilon\) sera multiplié par ce facteur.

class Trainer:
    def __init__(self, name=None, learning_rate=0.01, epsilon_decay=0.9999):
        self.state_size = 16
        self.action_size = 4
        self.gamma = 0.9
        self.epsilon = 1.0
        self.epsilon_min = 0.01
        self.epsilon_decay = epsilon_decay
        self.learning_rate = learning_rate
        self.name = name

Définition du réseau de neurone.

        if name is not None and os.path.isfile("model-" + name):
            model = load_model("model-" + name)
        else:
            model = Sequential()
            model.add(Dense(24, input_shape=(self.state_size,), activation='relu'))
            model.add(Dense(24, activation="relu"))
            model.add(Dense(self.action_size, activation='linear'))
            model.compile(loss='mse', optimizer=sgd(lr=self.learning_rate))

        self.model = model       

Les deux premières lignes sont utiles si l’on veut récupérer un modèle préexistant, enregistré sur le disque. La définition du modèle vient juste après :

model = Sequential() Ceci définit un réseau de neurone constitué de couches successives. Chaque couche que l’on va définir va prendre en entrée la couche précedemment définie.

    model.add(Dense(24, input_shape=(self.state_size,), activation='relu'))
    model.add(Dense(24, activation="relu"))
    model.add(Dense(self.action_size, activation='linear'))

Ici, nous ajoutons 3 couches : La première est constituée de 24 neurones, comme entrée le state (donc d’une taille state_size). L’activation est la fonction non linéaire qui filtre la sortie d’un neurone. Pour plus détail, vous pouvez lire http://cdancette.fr/2017/10/08/neural-nets/

La seconde couche (hidden layer) est également constituée de 24 neurones, et de la même fonction d’activation.

La dernière couche (final layer) possède 4 sorties (self.action_size), une pour chaque action. Pour un état donné en entrée, la valeur que nous renverra chaque neurone sera un tableau de taille 4, chaqun contenant la valeur estimée de cette action. Comme dans la parrtie précédente, nous choisirons alors l’action avec la valeur maximale.

Enfin, la ligne model.compile(loss='mse', optimizer=sgd(lr=self.learning_rate)) indique que la définition est terminée, et qu’on souhaite entrainer le réseau avec l’algorithme sgd (stochastic gradient descent). De plus, loss=mse indique que l’on souhaite utiliser la los “mean squared error”, ie que l’on souhaite minimiser l’erreur quadratique moyenne. D’autres loss sont utilisables, mais celle-ci est adaptée à la régression que l’on a ici.

Entrainement

Nous allons définir une autre méthode à notre classe Trainer:

class Trainer():

    ...

    def train(self, state, action, reward, next_state, done):
        target = self.model.predict(np.array([state]))[0]
        if done:
            target[action] = reward
        else:
            target[action] = reward + self.gamma * np.max(self.model.predict(np.array([next_state])))

        inputs = np.array([state])
        outputs = np.array([target])

        return self.model.fit(inputs, outputs, epochs=1, verbose=0, batch_size=1)

Dans cette fonction, nous définissions la base de l’algorithme du Q learning : la mise à jour de Q.

La formule est plus simple que dans le tutoriel précedent. En effet, la vitesse d’apprentissage (learning rate) n’apparait pas ici, car elle est incluse dans l’algorithme d’apprentissage, comme nous verrons plus tard. Nous définissions juste la valeur souhaitée de la valeur de Q pour cet état et cette action.

target = self.model.predict(np.array([state]))[0] Ici, nous récupérons la valeur prédite par le réseau, pour cet état. target est un tableau de taille 4.

     if done:
        target[action] = reward
    else:
        target[action] = reward + self.gamma * np.max(self.model.predict(np.array([next_state])))

Ici, nous choissions la valeur cible pour l’action que nous avons effectué (nous ne changeons pas la valeur pour les autres actions, puisque nous n’avons pas de donnée sur la reward que aurions obtenu). Si c’est l’état final, la cible est la récompense. Sinon, c’est la récompense, plus la meilleure valeur que nous pourrions obtenir avec l’action suivante (dégradée du facteur d’actualisation \(\gamma\))

    inputs = np.array([state])
    outputs = np.array([target])

    return self.model.fit(inputs, outputs, epochs=1, verbose=0, batch_size=1)

C’est ici que s’effectue l’apprentissage du réseau : nous indiquons au réseau que pour cet état, il doit renvoyer cette sortie. Le réseau va alors modifier légerement ses poids (par l’algorithme de backpropagation), pour se rapprocher de la sortie désirée.

Nous allons enfin définir une méthode qui nous renverra la meilleure action, pour un état donné. Cette fonction nous renverra un état aléatoire selon le paramètre d’exploration \(\epsilon\).

class Trainer():

    ...

    def get_best_action(self, state, rand=True):
        
        self.epsilon *= self.epsilon_decay

        if rand and np.random.rand() <= self.epsilon:
            # The agent acts randomly
            return random.randrange(self.action_size)
        
        # Predict the reward value based on the given state
        act_values = self.model.predict(np.array([state]))

        # Pick the action based on the predicted reward
        action =  np.argmax(act_values[0])  
        return action

D’abord, on multiplie epsilon par son facteur d’actualisation, de façon a diminuer progressivement l’aléatoire. On remarque que la fonction a un argument rand, qui indique si on souhaite une action possiblement aléatoire, ou la meilleure action possible (pas d’exploration).

Le mode rand=False nous servira lorsque le modèle sera entrainé, pour l’utiliser.

On retourne alors une action aléatoire avec une probabilité de \(\epsilon\), et sinon, la meilleure action. On utilise pour cela le réseau de neurone : self.model.predict(np.array([state])) nous renvoie les valeurs de chaque action, et il nous suffit de choisir l’action avec la valeur maximale.

# Lancement de l’entrainement

On définit une simple fonction train, qui va boucler sur le nombre d’itérations que l’on souhaite.

import time 

def train(episodes, trainer, game):
    scores = []
    losses = [0]

    for e in range(episodes):
        state = game.reset()
        score = 0  # score in current game
        done = False
        steps = 0  # steps in current game
        while not done:
            steps += 1
            action = trainer.get_best_action(state)
            next_state, reward, done, _ = game.move(action)
            score += reward
            trainer.train(state, action, reward, next_state, done)
            state = next_state
            if done:
                scores.append(score)
                break
            if steps > 200:
                trainer.train(state, action, -10, state, True) # we end the game
                scores.append(score)
                break
        if e % 100 == 0: # print log every 100 episode
            print("episode: {}/{}, moves: {}, score: {}"
                  .format(e, episodes, steps, score))
            print(f"epsilon : {trainer.epsilon}")
    return scores

Dans cette boucle se déroule l’algorithme d’apprentissage par renforcement : L’agent effectue une action (obtenue par trainer.get_best_action) récupère sa récompense, et le nouvel état. On entraine alors le réseau à associer le score de cet état et cette action à cette récompense par la fonction trainer.train.

On peut alors lancer l’algorithme d’apprentissage :

g = Game(4, 4, 0.1, alea=False) # Un jeu statique, avec 10% d'aléatoire dans les mouvements
g.print()

On obtient une grille de ce genre, ou le x représente l’agent, le o le puit, le ¤ le mur et le @ l’arrivée.

....
..¤x
..o.
@...

On lance alors l’entrainement :

trainer = Trainer(learning_rate=0.01)
score = train(2000, trainer, g)

Courbe de score en fonction de l’itération On peut afficher la courbe de score (ici moyennée sur 10 iterations successives)

import matplotlib.pyplot as plt
score = np.array(score)
score_c = np.convolve(score, np.full((10,), 1/10), mode="same")
plt.plot(score_c)
plt.show()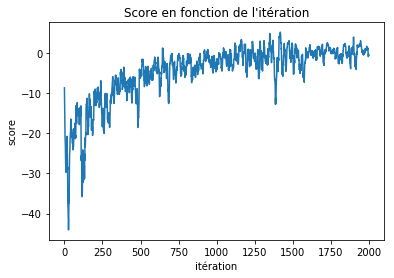

Nous pouvons maintenant afficher le résultat. On voit que l’agent a appris à éviter de passer à coté du trou : il préfère prendre le chemin le plus long, où la probabilité de tomber dedans est nulle.

state = g.reset()
state = g._get_state()
done = False
g.print()
while not done:
    time.sleep(1)
    # on selectionne l'action avec rand=False pour choisir toujours la meilleure
    action = trainer.get_best_action(g._get_state(), rand=False)
    next_state, reward, done, _ = g.move(action)
    g.print()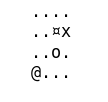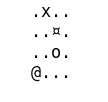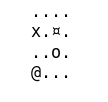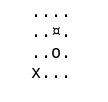

Conclusion

Vous pouvez retrouver tout le code décrit dans cet article sur github.

Nous avons donc appris comment définir un réseau de neurone simple, à l’entrainer, et à l’utiliser sur des nouveaux examples.

Dans une prochaine partie, nous verrons comment utiliser notre algorithme dans un jeu plus compliqué, où le terrain peut changer à chaque partie. L’algorithme devra alors apprendre à généraliser de manière à éviter les obstacles, et à trouver le meilleur chemin pour arriver à son objectif.

Cela nous ammenera à modifier la manière dont les données sont encodées, ainsi qu’à de nouveaux concepts comme le batching et l’experience replay pour améliorer les résultats.

Si vous avez aimé cet article, n’hésitez pas à m’envoyer un mail.