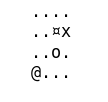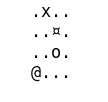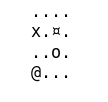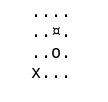
Le jeu

Un tutoriel pour apprendre le Q-learning sur un jeu simple. Dans cette première partie, on s’interesse au Q-learning stocké dans un tableau de valeurs. Par la suite, on utilisera des reseaux de neurones pour approximer cette table. Tous les codes présentés ici peuvent être trouvés sur github.

Qu’est-ce que le Reinforcement Learning, ou apprentissage par renforcement ?

C’est un type d’algorithme pour apprendre à un agent à maximiser ses gains dans un environnement ou chaque action lui donne une récompense (positive ou négative).

Plan

Partie 1 : jeu statique, le terrain ne change pas, utilisation d’un tableau de valeurs (sans réseau de neurones).
Partie 2 : Jeu statique, le terrain ne change pas, utilisation d’un réseau de neurone pour approximer la fonction de valeurs Q.
Partie 3 : Jeu dynamique, le terrain change à chaque partie : utilisation d’un réseau de neurones.

Description du jeu

Il s’agit d’un jeu inspiré par l’environnement Frozen Lake de gym, librairie créée par OpenAI, destinée à faciliter le travail de reinforcement learning. Ce jeu est aussi connu sous le nom de Grid World.

Jeu

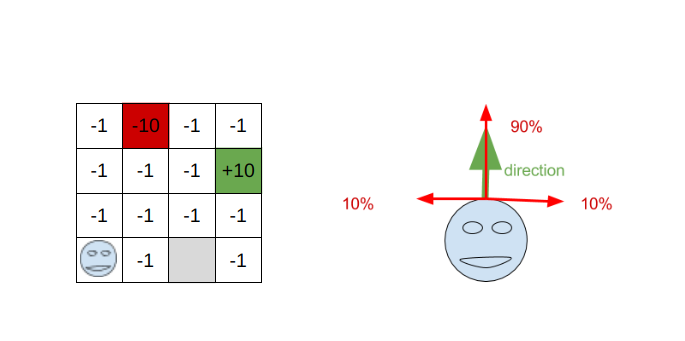
On dispose d’un agent situé sur une grille. La grille comporte 3 cases particulières : un mur (en gris), un puit (en rouge), et une arrivée (en vert). Si l’agent arrive sur le puit ou l’arrivée, le jeu se termine. Le joueur ne peut pas se déplacer sur le mur, et le joueur est récompensé de -1 à chaque fois qu’il arrive sur une case non colorée.

L’environnement peut être doté d’une composante aléatoire : à chaque choix de mouvement (haut, bas, gauche ou droite), l’agent pourra se déplacer dans une direction non voulue. Ce comportement est paramétrable.

Notre but va donc être de maximiser la somme des récompenses obtenues par l’agent au cours de sa partie.

Le code de l’environnement :

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
import random


class Game:
    ACTION_UP = 0
    ACTION_LEFT = 1
    ACTION_DOWN = 2
    ACTION_RIGHT = 3

    ACTIONS = [ACTION_DOWN, ACTION_LEFT, ACTION_RIGHT, ACTION_UP]

    ACTION_NAMES = ["UP", "LEFT", "DOWN", "RIGHT"]

    MOVEMENTS = {
        ACTION_UP: (1, 0),
        ACTION_RIGHT: (0, 1),
        ACTION_LEFT: (0, -1),
        ACTION_DOWN: (-1, 0)
    }

    num_actions = len(ACTIONS)

    def __init__(self, n, m, wrong_action_p=0.1, alea=False):
        self.n = n
        self.m = m
        self.wrong_action_p = wrong_action_p
        self.alea = alea
        self.generate_game()



    def _position_to_id(self, x, y):
        """Donne l'identifiant de la position entre 0 et 15"""
        return x + y * self.n

    def _id_to_position(self, id):
        """Réciproque de la fonction précédente"""
        return (id % self.n, id // self.n)

    def generate_game(self):
        cases = [(x, y) for x in range(self.n) for y in range(self.m)]
        hole = random.choice(cases)
        cases.remove(hole)
        start = random.choice(cases)
        cases.remove(start)
        end = random.choice(cases)
        cases.remove(end)
        block = random.choice(cases)
        cases.remove(block)

        self.position = start
        self.end = end
        self.hole = hole
        self.block = block
        self.counter = 0
        
        if not self.alea:
            self.start = start
        return self._get_state()
    
    def reset(self):
        if not self.alea:
            self.position = self.start
            self.counter = 0
            return self._get_state()
        else:
            return self.generate_game()

    def _get_grille(self, x, y):
        grille = [
            [0] * self.n for i in range(self.m)
        ]
        grille[x][y] = 1
        return grille

    def _get_state(self):
        if self.alea:
            return [self._get_grille(x, y) for (x, y) in
                    [self.position, self.end, self.hole, self.block]]
        return self._position_to_id(*self.position)

    def move(self, action):
        """
        takes an action parameter
        :param action : the id of an action
        :return ((state_id, end, hole, block), reward, is_final, actions)
        """
        
        self.counter += 1

        if action not in self.ACTIONS:
            raise Exception("Invalid action")

        # random actions sometimes (2 times over 10 default)
        choice = random.random()
        if choice < self.wrong_action_p:
            action = (action + 1) % 4
        elif choice < 2 * self.wrong_action_p:
            action = (action - 1) % 4

        d_x, d_y = self.MOVEMENTS[action]
        x, y = self.position
        new_x, new_y = x + d_x, y + d_y

        if self.block == (new_x, new_y):
            return self._get_state(), -1, False, self.ACTIONS
        elif self.hole == (new_x, new_y):
            self.position = new_x, new_y
            return self._get_state(), -10, True, None
        elif self.end == (new_x, new_y):
            self.position = new_x, new_y
            return self._get_state(), 10, True, self.ACTIONS
        elif new_x >= self.n or new_y >= self.m or new_x < 0 or new_y < 0:
            return self._get_state(), -1, False, self.ACTIONS
        elif self.counter > 190:
            self.position = new_x, new_y
            return self._get_state(), -10, True, self.ACTIONS
        else:
            self.position = new_x, new_y
            return self._get_state(), -1, False, self.ACTIONS

    def print(self):
        str = ""
        for i in range(self.n - 1, -1, -1):
            for j in range(self.m):
                if (i, j) == self.position:
                    str += "x"
                elif (i, j) == self.block:
                    str += "¤"
                elif (i, j) == self.hole:
                    str += "o"
                elif (i, j) == self.end:
                    str += "@"
                else:
                    str += "."
            str += "\n"
        print(str)

Partie 1 : Un terrain fixe.

Dans ce tutoriel, on va s’intéresser dans un premier temps à un terrain fixe : la position des éléments ne sera pas modifiée entre chaque partie. Notre algorithme pourra alors apprendre la structure du terrain par coeur, pour pouvoir déplacer l’agent correctement.

Il y a 16 états possibles dans l’environnement, on les numerotera donc de 0 à 15, et 4 actions possibles à chaque étape. Une action “impossible” renverra un état identique à l’état précédent.

Q learning avec une table

Le Q-learning consiste à déterminer une fonction Q(s, a) qui prend deux paramètres :

s : L’état du système
a : l’action que l’on veut effectuer

Et cette fonction renvoie une valeur, qui est la récompense potentielle que l’on obtiendra à long terme en choisissant cette action.

Ici, nous aurons un faible nombre d’états et d’actions (16 et 4), donc nous pouvons stocker toutes les valeurs dans un tableau. C’est la méthode la plus précise, lorsque la mémoire le permet. Si le nombre d’état / actions devient trop grand, il sera nécessaire d’approximer la fonction, comme on le verra dans une autre partie.

Algorithme d’apprentissage

L’algorithme nous permettra de remplir ce tableau de Q-values, pour pouvoir déterminer, à chaque état, l’action optimale (qui sera en fait la valeur maximale obtenue parmi toutes les actions possibles).

Nous commencons avec un tableau vide, de taille 16 x 4 (16 états, 4 actions).

Puis, nous lançons l’agent, avec des mouvements aléatoires, et à chaque étape, nous pouvons mettre à jour le tableau grâce à cette formule

Formule todo simplifier la formule

C’est cette formule qui constitue le coeur du Q-learning. On va actualiser la valeur de Q(s, a) grâce à la récompense effectivement obtenu depuis l’état s en appliquant l’action a, à laquelle on va ajouter la meilleure récompense qu’on pourra obtenir dans le futur.

On implémente ce qu’on vient d’expliquer

# q learning with table
import numpy as np

states_n = 16
actions_n = 4
Q = np.zeros([states_n, actions_n])

# Set learning parameters
lr = .85
y = .99
num_episodes = 1000
cumul_reward_list = []
actions_list = []
states_list = []
game = Game(4, 4, 0) # 0.1 chance to go left or right instead of asked direction
for i in range(num_episodes):
    actions = []
    s = game.reset()
    states = [s]
    cumul_reward = 0
    d = False
    while True:
        # on choisit une action aléatoire avec une certaine probabilité, qui décroit
        # TODO : simplifier ça (pas clair)
        Q2 = Q[s,:] + np.random.randn(1, actions_n)*(1. / (i +1))
        a = np.argmax(Q2)
        s1, reward, d, _ = game.move(a)
        Q[s, a] = Q[s, a] + lr*(reward + y * np.max(Q[s1,:]) - Q[s, a]) # Fonction de mise à jour de la Q-table
        cumul_reward += reward
        s = s1
        actions.append(a)
        states.append(s)
        if d == True:
            break
    states_list.append(states)
    actions_list.append(actions)
    cumul_reward_list.append(cumul_reward)

print("Score over time: " +  str(sum(cumul_reward_list[-100:])/100.0))

game.reset()
game.print()

Explications lignes par lignes

states_n = 16
actions_n = 4
Q = np.zeros([states_n, actions_n])

On définit le nombre d’états (16), et d’actions pour chaque état (4). Et on construit le tableau de valeur etat / action Q, rempli de 0.

# Set learning parameters
lr = .85
y = .99
num_episodes = 1000

On définit les paramètres de l’apprentissage.

lr : learning rate, c’est la vitesse d’apprentissage. Plus il est élevé, plus les nouvelles informations seront importantes par rapport aux anciennes. À 0, l’agent n’apprend rien, et à 1, il ne retiendra pas les anciennes infos qu’il a apprises. C’est l’idéal si l’environnement est déterministe (ie 1 etat + 1 action = toujours le même état et la même récompense). Ici l’environnement n’est pas déterministe, car l’agent peut se tromper de direction. On le place donc à .85 (valeur trouvée par tatonnement).

y : facteur d’actualisation (gamma), entre 0 et 1. : détermine l’importance des récompenses futures. Trop élevé (trop proche de 1), il y a risque de divergence.

num_episodes : le nombre de parties que l’on va faire. 1000 est largement suffisant ici, comme on peut le voir dans les graphiques plus bas.

    actions = []
    s = game.reset()
    states = [s]
    cumul_reward = 0
    d = False

Initialisation du jeu

    Q2 = Q[s,:] + np.random.randn(1, actions_n)*(1. / (i +1))
    a = np.argmax(Q2)

Etape importante : ici, on choisit quelle action on va effectuer pour ce tour. On a une probabilité \({1/(i+1)}\)de faire une action aléatoire (i = 0 au début, donc l’action est forcément aléatoire). Puis cette probabilité décroit au cours du temps.

    Q[s, a] = Q[s, a] + lr*(reward + y * np.max(Q[s1,:]) - Q[s, a]) # Fonction de mise à jour de la Q-table

On applique la formule du Q-learning.

Performances

On peut afficher plusieurs graphiques pour calculer les performances de notre algorithme. Une courbe pertinente est l’évolution des récompenses cumulées (ie le score total à la fin de la partie). En effet, le Q-learning est confectionné pour maximiser cette récompense cumulée.

import matplotlib.pyplot as plt
plt.plot(rList[:100])
plt.ylabel('Cumulative reward')
plt.xlabel('Étape')
plt.show()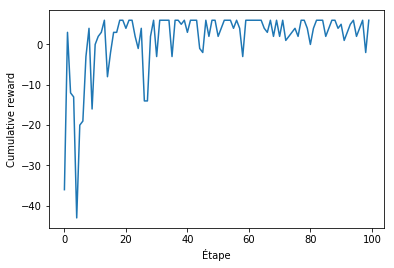

Graphique de la reward totale

On voit ainsi que l’on arrive assez rapidement à un maximum. Le score n’est jamais parfait car il y a de l’aléatoire dans le jeu (l’agent se trompe de direction 2 fois sur 10), ce qui fait qu’il tombe parfois dans le trou.

Un example, on voit que l’agent évite le trou (représenté par un O).

Jeu

La suite : Partie 2 : environnement qui change entre chaque partie + réseaux de neurones

Partie 2

Si vous avez aimé cet article, n’hésitez pas à m’envoyer un mail.

Resources (en anglais)

https://medium.com/emergent-future/simple-reinforcement-learning-with-tensorflow-part-0-q-learning-with-tables-and-neural-networks-d195264329d0
http://outlace.com/rlpart3.html
https://mpatacchiola.github.io/blog/2016/12/09/dissecting-reinforcement-learning.html
https://medium.com/@awjuliani/super-simple-reinforcement-learning-tutorial-part-1-fd544fab149